Opgaver i tal og regning
201
Angiv på en tallinje løsningsmængden til uligheden x < 6 (læses x mindre end 6) a) når x ∈ N (N er mængden af Naturlige tal)
![]()
b) når x ∈ Z (Z er mængden af hele tal)
![]()
c) når x ∈ R (R er mængden af de reelle tal)
![]()
![]()
b) når x ∈ Z (Z er mængden af hele tal)
![]()
c) når x ∈ R (R er mængden af de reelle tal)
![]()
Omskriv til titals potenser:
a) 60.000
b) 400.000
c) 3 millioner
d) 8 milliarder
Omskriv til titals potenser:
a) 0,00251
b) 0,0000005
c) 0,0000000091
d) 0,000812
Omskriv til titals potenser:
a) 149 000 000
b) 456 millioner milliarder
c) 7560000000
d) 0,0000000502
Omskriv til titals potenser med ét ciffer efter kommaet:
Eksempel: 36.764 = 3,7 · 104
a) 63.568
b) 482.934
c) 3.425.563
d) 81.714.958
Omskriv til titals potenser med ét ciffer efter kommaet:
Eksempel: 0,000000362 = 3,6·10-7
a) 0,0056921
b) 0,000000000004927
c) 0,00003492
d) 0,000000008171
Omskriv til kommatal:
a) 5,01·108
b) 1,2·104
c) 4,86·10-6
d) 6,33·10-9
Omskriv med passende præfikser.
Eksempel: 34.000 m = 34 · 103 = 34 km
a) 5,01·109 Joule
b) 1,2·1012 byte
c) 4,86·10-6 gram
d) 6,33·10-9 meter
e) 2.411 meter
f) 0,0045 meter

Virus er mellem 20 nm og 400 nm i diameter.
nm læses nanometer.
Beregn:
a) 25-9·4-3·2+12
b) 20:5+8:2-4·3
c) 4·3²+4·10-25
d) 18:3²+33
e) 15+2³:4+2
Beregn:
a) (5-8:2+5)·(2+1)
b) (6+2·2)²
c) (11-7)·3³
d) 30-(14+20)-(2-9)
e) 28-(-2)-(5-9)
Forkort brøken mest muligt:

Forlæng brøken
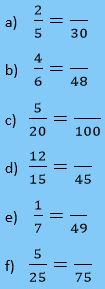
Læg brøkerne sammen, og forkort brøken:

Læg brøkerne sammen, og forkort brøken:

Læg brøkerne sammen, og forkort brøken:

Træk brøkerne fra hinanden, og forkort brøken:

Udregn:

Udregn uden lommeregner. Se, om du kan finde frem til en smart metode, så du undgår, at skulle regne med for store tal.

Kan du huske og bruge det, du har lært om brøker?
Udregn, og forkort, hvis det er muligt:

Kan du huske og bruge det, du har lært om brøker?
Udregn, og forkort, hvis det er muligt:

Gang ind i parentesen
a) 2(4a+3) =
b) (a+8)·5 =
c) 5(3x-4) =
d) 2(3x+1) =
Gang ind i parentesen
Eksempel: -3(a+b) = (-3)·a+(-3)·b = -3a-3b
a) -2(3x+5) =
b) -6(a+7b) =
c) (4a+8b)(-3) =
d) -a(3b+1) =
Gang ind i parentesen
a) 5a(2a+7+3b) =
b) -3x(2x²+3x-5) =
c) (4a+5b+c)(-7) =
d) 4x²(2x+6y) =
Gang ind i parentesen
a) a(b+c-e) =
b) ab(a+ab+c) =
c) x²(2x+5+3y) =
d) -5a(2b+6) =
e) -5b(2b+8) =
Sæt så meget uden for parentes som muligt:
a) 2x+2y =
b) 12ab-12ac =
c) 4ac-4bc+8c =
d) xyz+xy =
Sæt så meget uden for parentes som mligt:
a) (a+b)x+(a+b)y =
b) a²b+ab²
c) xab+12ab =
Gang parenteserne:
a) (a+2)(b+7) =
b) (x+1)(ab+7) =
c) (a+3)(b- 9) =
d) (a+x+5)(b+8) =
Gang parenteserne:
a) -(x+2)(y+2) =
b) -2(3x+4)(5-2y) =
c) -(a+x+5)(b+c) =
d) -5x(x-2)(y+6) =
Undersøg, om x=4 er en løsning til ligningerne:
a) 3x+5=17
b) -2x+20=12
c) 3x+1=20
d) -6x+24=0
Undersøg, om x=2 er en løsning til ligningerne:
a) x²-7x+10=0
b) 2x²-4x-6=0
c) 3x²-12x+12=0
Løs ligningerne, og skiv undervejs en kommentar som for eksempel:
Lægger 3 til på begge sider
Trækker 5x fra på begge sider
Ganger med 2 på begge sider
Dividerer med 4 på begge sider
Reducerer på højre side
a) x-19=9
b) 3x-1=11
c) 2x-6=4
d) 20=8+2x
e) 4x+23=3+8x
f) 4x-7= -2x+11
Husk at gøre prøve.
Løs ligningen:
a) x+(16+4x)-30=6
b) 14y+8=16y+3
c) 6(x+3)=x+3(4-x)-2
d) 6x+(x-3)=11
e) 4(2x+1)-12=16
Husk at gøre prøve.
Løs ligningerne:
a) 5x-(3x-1)=11
b) 22x-(-3+15x)+1=32
c) 2-(8-a)=4a+3(3a-6)
d) x²+3(x-4)=x(x+2)-12
Husk at gøre prøve.
Løs ligningerne – måske er det en god idé, at minde dig selv om, hvad det vil sige, at løse en ligning!
a) 5(2+x) – 2x = 3(x+1)+4
b) 4x–9 = 2(2x-4)-1
Reducer udtrykket:
a) (x+3)(x+3) =
b) (4+x)² =
c) (4-x)² =
c) (x-2)² =
Reducer:
a) (2a+3)² =
b) (x+4y)² =
c) (6x-2)² =
Løs ulighederne:
a) 5-x<4
b) 2x-5<1
Løs ulighederne og illustrer løsningsmængden på tallinjen:
a) 3(x-1) + 2(x-1) ≤ 7x + 7
![]()
b) -7x > -28
![]()
Løs uligheden og illustrer løsningsmængden på tallinjen:
![]()
![]()